在动力和航空航天等领域,设备一般都有复杂曲面和自由曲面零件,既要求有很高的几何精度,还对加工表面形貌特征和物理性能有要求,而提高精度最重要的是加工过程误差(主要是热误差和力误差)和几何误差因素。现有的误差测试与分离技术测试过程复杂,费时且成本高,大多是间接测试机床而非直接测试工件,生产现场很少采用。Denavit和Hartenberg[3]于1955年建立了著名的D-H法,是分析运动机构在空间运动姿态的有力工具。Srivastava等[4]在一台RRTTT型的五轴机床上建立了基于HTM方法的综合误差模型,在分别得到几何误差和热误差元素之后,可计算出各进给轴的补偿量,对机床的空间误差进行补偿。天津大学刘又午教授[5]将多体系统理论引入数控机床建模,并对误差辨识应用9线法进行解决。
国防科技大学粟时平博士对机床多体系统运用拓扑结构进行概括,并用低序体阵列进行描述,用特征矩阵表达了机床相邻体之间的位姿,并以三轴、五轴机床为例给出了理想运动模型、有误差运动模型和空间误差模型等的具体表达式。上海交通大学杨建国等针对数控机床的误差概念、误差形成机理及误差建模等进行了研究,并在误差补偿上有了重大突破。上海交通大学刘国良等开发了一种数控机床几何误差综合建模专家系统,可实现不同类型三轴加工中心的综合误差自动建模。东北大学刘春时等提出一套基于多体系统理论的五轴数控机床空间误差建模流程,并以某VMC650高速铣削五轴加工中心为对象验证了有效性。上海交通大学姜辉提出了一种热误差建模方法和误差补偿方法,并以FA-32M型铣床为研宄对象进行了验证。清华大学李铁民针对机床热误差建模进行了研究,探讨了热误差建模的两种方法(经验热误差建模和理论热误差建模)的优缺点。北京航空航天大学刘强等提出一种适合机床动态分析的拓展传递矩阵建模方法,简化了机床动力学建模过程,更适合工程应用。
在特征样件方面研究的领域很多,山东大学刘战强提出了基于高速切削加工工件测试的误差分离和误差补偿研究,但仅针对车床的加工样件,且试验只是定性试验。哈尔滨工业大学赵磊等提出了基于特征样件的方式来分离机床的几何误差研究,但仅考虑了几何误差,未针对加工误差。湖南科技大学赵前程提出一种基于形状误差的特征模型,在误差估计方法的准确度和不确定度上有很大优势,但仅从优化方法上进行考虑。
本文基于特征样件就几何误差进行分离,并可分离出加工过程误差。在此方案中,应用了在机测量系统,避免工件二次装夹,同时检测、设计与加工过程紧密结合,有利于保证加工精度和降低废品率。
2 误差分离原理
加工工件的总误差E一般将其定义为实际测量尺寸Drea与理想模型Dper之间的差值,即

加工后工件的实际测量尺寸很难达到理想值。
一般工件加工完成后会从机床取下,放置在三坐标测量仪上进行精度检测,即进行离线测量。三坐标测量仪的测量精度一般高于加工要求的尺寸公差一个数量级,测得数值可看作实际尺寸Drea。
Mou和Liu经试验研究证明,工件加工后离线测量尺寸与在线测量尺寸的差异等于机床的定位误差,当试验条件为室温状态时,此差异就是机床的几何误差,即
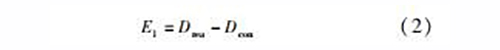
式中,Dcon为室温在机测量所得数值。
3 机床几何误差建模
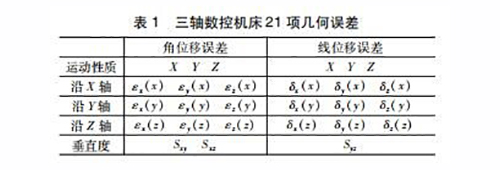
建立数控机床几何误差综合模型,首先要分析机床的几何误差参数,以大连机床VDL-1000E型数控铣床为例,共有21项几何误差参数(见表1)。
选择测量点时,首先进入在机测量软件,根据测量对象自动确定测量点选择方式,生成待测量点,去除缺陷点,最后提取测量点信息。根据规划好的测量点,测量各点的X、Y、Z坐标值来编写测量程序。本文利用UG二次开发编写在机测量软件,并将其编入在机测量软件中。
(1)建立三轴数控机床模型
图1为该三轴数控机床的结构示意图,工件通过夹具安装在X轴上,主轴安装在Z轴上。
(2)建立拓扑结构及坐标系
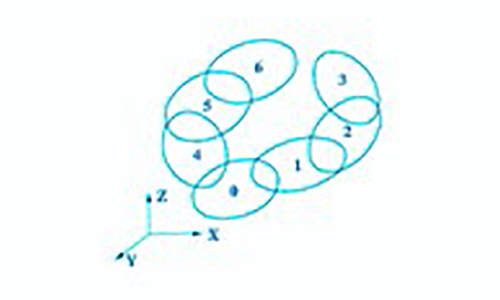
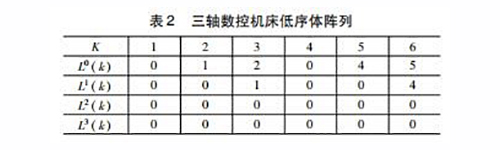
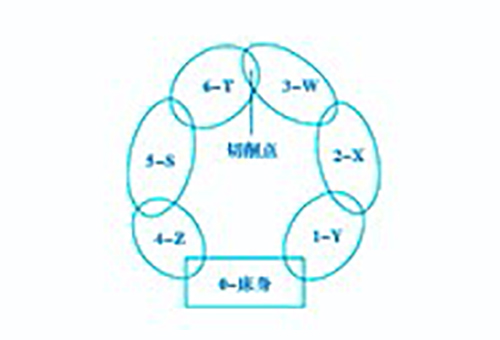
三轴机床的拓扑结构如图2所示,其低序体阵列见表2。首先在床身(惯性体0)上建立参考坐标系O0X0Y0Z0,然后按远离床身的位置分别建立坐标系O1X1Y1Z1、O2X2Y2Z2、O3X3Y3Z3、O4X4Y4Z4、O5X5Y5Z5、O6X6Y6Z6。为了降低模型的复杂性,设坐标系OkXkYkZk(k=1,2,… 6)与参考坐标系O0X0Y0Z0重合。
(3)三轴数控机床的综合误差模型
为方便分析,建立机床运动链示意图帮助理解(见图3)。
三轴数控机床空间几何误差综合模型为
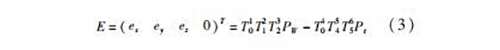
基于小误差理论,略去误差的二阶以上项并对公式(3)进行化简,得
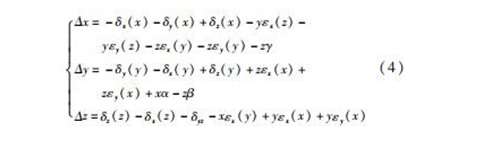
4 01203 建模仿真
使用MATLAB对公式(4)进行仿真。由图4可知,x项综合误差随y有小幅变化,随x波动式的增加,在整个行程内沿负方向呈递增趋势。由图5可知,y项综合误差随x有小幅变化,随y波动式的增加,在整个行程内呈递增趋势。如图6所示,总误差总体上随着远离设置的原点位置逐渐变大。



5 试验分析
本试验采用的数控加工系统为大连机床厂生产的立式数控加工中心VDL-1000E。在机测量系统作为测量时数据的记录载体,基本参数如下:X行程1200mm、Y行程560mm、Z行程600mm,刀库容量20把,主轴最高转速为800r/min,定位精度全程±0012mm,重复定位精度为±0.008mm。采用应用广泛、功能全性能好的FANUC0i-MD系统,并对外提供RS232外部控制接口,具有自己的宏编程语言,方便程序的编程调用。


测量的工件采用轿车覆盖件的凸模进行试验,验证整个系统的通用性和测量精度。测量选择轿车覆盖件上的自由曲面部分进行测量,模具凸凹模的实体见图7。
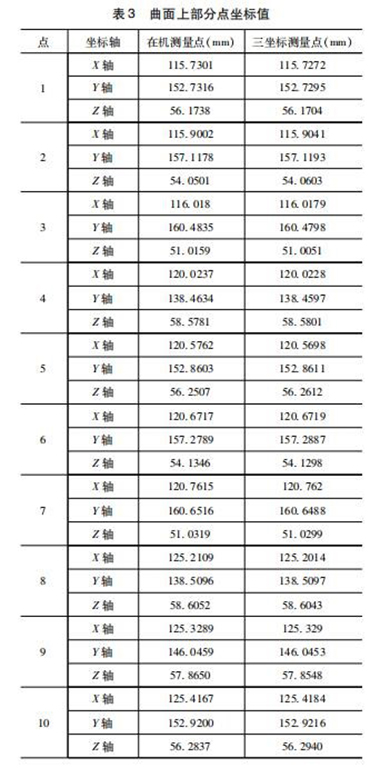
试验数据对比:选取的数据点位置如图8所示,采用在机测量和三坐标测量机测量所得数据整理后,曲面部分点坐标值数据见表3。
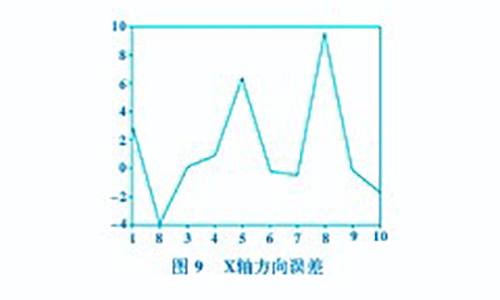
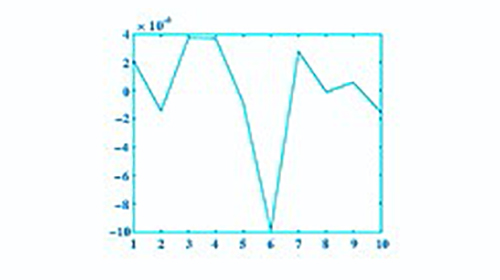
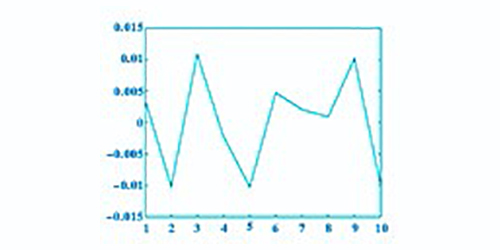
根据MATLAB软件分析获取的数据,X、Y、Z轴方向的误差分别如图9、图10和图11所示。由实际数据测量得到plot图,虽然选取的数据较少,但可以看出实际与预测趋势一致。
6 结语
基于多体系统理论对三轴数控机床的几何误差进行划分,建立了拓扑结构,揭示了各个体之间的关系,进而推导出三轴数控机床的空间误差模型,并利用三坐标测量机和在机测量系统分离出几何误差。
136-0043-0755
